Notatka na marginesie

exp(x) = sin(x)

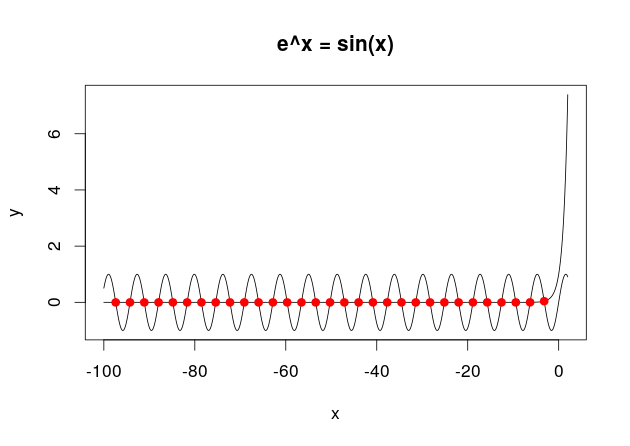
Some function
f(x) = e^x-\sin(x)
gives us interesting properties:

  • on the left side (x<0) we have f(x) \approx \sin(x) and having infinitely many zeros
  • on the right side (x>0) we have f(x) \approx e^x and growing exponentially

However, there is POI about zeros of this function:

exsinx




Since \sin(x) \approx x when x is small, we have approximation of first root as an solution of e^x = - \pi - x
x_1 \approx - \pi - e^{-\pi - e^{-\pi - e^{-\pi - \ldots}}} = -W(e^{-\pi})-\pi \approx -3.18305
where W(x) is Lambert-W function.
The same way we have approximation of second root as an solution of e^x = 2\pi + x x_2 \approx - 2\pi + e^{-2\pi + e^{-2\pi + e^{-2\pi + \ldots}}} = -W(e^{-2\pi})-2\pi \approx -6.28131
We know that e^x \rightarrow 0 as x \rightarrow - \infty there is x_n \rightarrow -n\pi, although we don’t know the exact solution yet..

Obrazek

Valentines

Układ na 13×13 po ruchach: OP U2 l4:5 R4:5 u2 L4:5 r4:5
U3 l3:6 R3:6 u3 L3:6 r3:6
U4 l2:4 R2:4 l6:8 u4 L2:4 r2:4 L6:8
U5 l2:3 R2:3 l7 u5 L2:3 r2:3 L7
U6 l2:3 R2:3 u6 L2:3 r2:3
U7 l2:4 R2:4 u7 L2:4 r2:4
U8 l3:5 R3:5 u8 L3:5 r3:5
U9 l4:6 R4:6 u9 L4:6 r4:6
d4 l5:9 D4 L5:9
d3 l6:8 D3 L6:8
d2 l7 D2 L7
Continue reading →